¿Qué es el Interés Simple? (Fórmulas y Ejercicios Resueltos)

La forma más sencilla de calcular los intereses es a través del Interés Simple, a su vez es importante comprender que a través de esta fórmula se puede identificar el valor del dinero a través del tiempo.

Este interés se utiliza en el sistema financiero informal, por los prestamistas particulares y prendarios, esto porque a través de este interés no se permite la capitalización de los intereses por lo que resulta siendo menor que el Interés Compuesto, esto debido a que mientras este último interés es variable, el Interés Simple es constante.

¿Qué es el Interés Simple?

El interés es simple únicamente cuando sólo el capital gana intereses por todo el tiempo que dura la transacción, entendiendo, así como explica Jhonny de Jesús Meza Orozco en su libro Matemáticas Financieras aplicadas (2011) “Se llama interés simple aquél en el cual los intereses devengados en un período no ganan intereses en los períodos siguientes, independientemente de que se paguen o no. Únicamente sobre el capital principal se liquidan los intereses sin tener en cuenta los intereses precedentes causados. La liquidación de los intereses se hace sobre el saldo insoluto, es decir, sobre el capital no pagado” (pág. 32).

El Interés Simple es el interés vencido al final del plazo.

Fórmula

Los elementos que intervienen en una operación de interés simple con sus respectivos significados son los siguientes:

I = Cit

Capital Inicial (C): Llamado también principal, presente o actual, suele representarse también con las letras A o P (valor presente). Es el dinero que se invierte en un inicio. Generalmente se toma como referencia el inicio del periodo.

Interés simple o generado (I): Es el monto de intereses generados en un determinado periodo. Es el importe monetario del interés que genero el capital a lo largo del tiempo.

Tasa de interés (i): Representa el costo, rendimiento o lo que se produce de un capital, ya sea producto de un préstamo o cantidad que se invierte.

Tiempo (n/t): Es el lapso (años, meses, días, etc.) que permanece prestado o invertido un capital.

Tipos

Al realizarse este tipo de cálculos financieros en las que involucran variables como tiempo y tasa de interés, surge la duda de que días se deben tomar para el año, es decir, si se tienen que tomar 360 días o 365 días, por lo que esto da origen a dos tipos.

Ordinario o comercial

También se le conoce como aproximado y se calcula con base en un año de 360 días, simplifica algunos cálculos, sin embargo, aumenta el interés cobrado por el acreedor.

Normalmente los bancos acostumbran a calcular los intereses, tomando como base el año de 360 días.

Exacto o Real

Este por su parte se calcula con el año de calendario de 365 días o de 366 días si se tratara de un año bisiesto.

Cálculo del tiempo

Cuando se conocen las fechas, para calcular el número de días, el interés puede calcularse de las siguientes formas:

Cálculo del tiempo exacto

En este cálculo se toma como referencia el número de días del calendario, es el número exacto de días que se encuentran en este, es decir los meses que tiene 30 días, 31 días y febrero cuando tiene 28 o 29 días.

Cálculo tiempo del tiempo aproximado

En este caso se utiliza para facilitar el cálculo de tiempo, suponiendo que cada mes tiene 30 días.

Para ejemplificar la determinación del tiempo a continuación se presenta el conteo de días con ambos métodos para un crédito del 08 de octubre del 2020 al 25 de febrero del 2021:

Ejemplo de Interés Simple

Para ejemplificar el cálculo del Interés Simple Exacto y Ordinario, tanto con la estimación de tiempo aproximado como exacto, analice los intereses de una deuda de $20 000 000 a una tasa de interés anual de 29%, formalizada el 14 de noviembre del 2020 y que vence el 25 de febrero del 2021.

Valor Futuro

Valor nominal de una inversión más los intereses ganados durante el periodo de tiempo de esta, también se conoce como el valor al vencimiento, y valor acumulado, generalmente se representa con la letra S o la F.

Este valor consiste en calcular el valor futuro, equivalente del valor presente, después de n/t períodos a una tasa de interés simple (i).

En resumidas cuentas, el valor futuro es igual al capital prestado más los intereses.

Fórmula de Valor Futuro

S = C (1+it)

Valor Presente

Es el valor de una deuda, en una fecha anterior a la de su vencimiento, este valor consiste en calcular el valor presente equivalente de un valor futuro, ubicado en n/t de períodos adelante a una tasa de interés simple (i).

En otras palabras, se refiere al valor actual de una cantidad futura de dinero, o una serie de pagos, evaluada a una tasa de interés dada.

Fórmula de Valor Presente

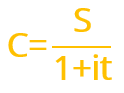
Fórmulas para calcular el Interés Simple

Ejercicios de Interés Simple con su respectiva solución

• Armando pidió prestado $250 000 a pagar en 20 meses. Si la tasa de interés es del 28,5% anual. ¿Qué cantidad deberá pagar por concepto de intereses?

• Calcular el interés comercial y real de $3 000 000 a una tasa de interés anual simple de 43% durante 130 días.

• ¿Cuánto acumula en 4 años en su cuenta bancaria Javier, si invierte $40 000 ganando intereses del 9,8% simple anual?

• Un pagaré por $56 000 con interés simple del 13,4% vence en 3 años, pero es vendido por su acreedor once meses antes de su vencimiento, con una tasa del 14,8%.

• Determine el interés exacto y ordinario sobre $28 000 al 12,7%, del 20 de abril al 1 de julio del 2020, calculando el tiempo en forma exacta y aproximada.

Síguenos en nuestras redes sociales estamos como @TodoGerencia en los siguientes enlaces: Instagram, Facebook, Pinterest, Telegram & Twitter.

Documentos de consulta

Ayres, F. (1991). Matemáticas Financieras (Primera ed.). Naucalpan de Juárez, México: McGraw-Hill Interaméricana.

Díaz Mata, A., & Aguilera Gómez, V. (2013). Matemáticas financieras (Quinta ed.). México D.F., México: McGRAW-HILL.

Meza Orozco, J. (2011). Matemáticas Financieras aplicadas (Cuarta ed.). Bogotá, Colombia: Ecoe Ediciones.

Vidaurri Aguirre, H. (2017). Matemáticas Financieras (Sexta ed.). México D.F., México: Cengage Leaning.

Villalobos, J. (2007). Matemáticas financieras (Tercera ed.). México D.F., México: Pearson Educación.