¿Qué es el Interés Compuesto? (Fórmulas y Ejercicios Resueltos)

¿Qué es el interés compuesto? Es necesario entender antes de contestar la interrogante que el tiempo y el dinero son dos factores que están estrechamente vinculados con los negocios y la vida de las personas, por lo que un ejemplo de esto son las cuentas de ahorro, ya que cuando se generan excedentes de efectivo, se ahorran durante un período determinado a fin de ganar un interés que aumente el capital original disponible; en otras ocasiones, en cambio, se tiene necesidad de recursos financieros como deudas durante un tiempo y se debe pagar un interés por su uso.

Entendiendo que en periodos cortos por lo general se utiliza, como ya se vio en el artículo anterior el Interés Simple. En periodos largos, sin embargo, se utilizará casi exclusivamente el Interés Compuesto.

¿Qué es el interés compuesto?

La expresión interés sobre interés tiene su fundamento en el Interés Compuesto, aplicado principalmente en las cuentas de ahorro a plazo de las entidades financieras y fondos de inversión.

Por lo que en el interés compuesto los intereses que se generan se suman al capital original en periodos establecidos y, a su vez, van a generar un nuevo interés adicional en el siguiente lapso.

“Si en cada intervalo de tiempo convenido en una obligación se agregan los intereses al capital, formando un monto sobre el cual se calcularán los intereses en el siguiente intervalo o periodo de tiempo, y así sucesivamente, se dice que los intereses se capitalizan y que la operación financiera es a interés compuesto”

(Portus Govinden, 1997, pág. 93)

En otras palabras, el interés compuesto se puede definir como la operación financiera en la cual el capital aumenta al final de cada período por adición de los intereses vencidos.

Conceptos básicos

Capitalización: Es definido como el proceso mediante el cual los intereses que se van originando de manera periódica se suman al capital anterior.

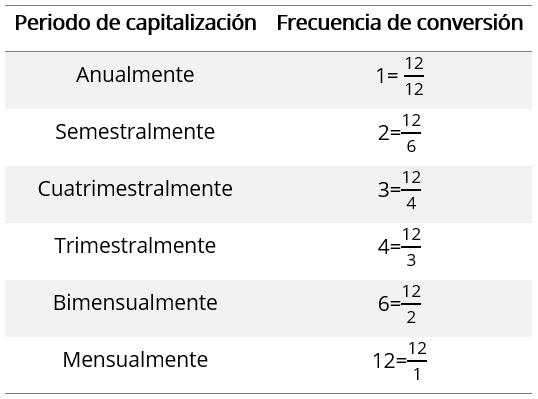
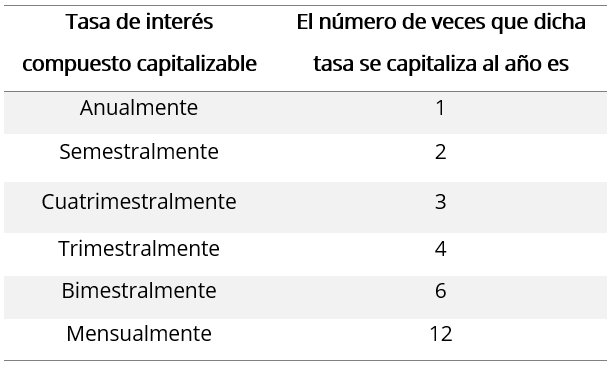
Periodos de capitalización: El interés se puede convertir en capital anual, semestral, cuatrimestral, trimestral, bimensual, mensual, quincenal, entre otros. Es así como a dicho periodo se le conoce como “periodo de capitalización”.

Frecuencia de conversión: También se le conoce como frecuencia de capitalización y se refiere al número de veces que el interés se capitaliza durante un año.

Valor futuro o monto compuesto de un capital a interés compuesto

Este valor se refiere al capital final, o bien capital acumulado, después de añadir el interés sucesivamente. Es así como en las operaciones de interés compuesto el valor al vencimiento también se suele llamar monto compuesto, principalmente por su característica fundamental de que el interés se convierte en capital durante un año.

Fórmula del monto compuesto

Sobre la fórmula de interés compuesto se debe aclarar que la tasa de interés a utilizar se debe emplear de acuerdo con la frecuencia de conversión de la obligación financiera, es decir, calcular la tasa de interés correspondiente al periodo de conversión.

S= C (1+i) ⁿ

S (M, F) = Monto compuesto en la fecha de vencimiento, también conocido como valor futuro, y contempla el valor nominal más los intereses ganados durante el plazo de la operación.

C (P) = Capital original o valor nominal de la obligación financiera.

n= Número de periodos de conversión, se calcula al multiplicar los años de la operación por la frecuencia de conversión.

(Años x Frecuencia de conversión)

i= Tasa de interés por periodo de conversión, esta se determina al dividir la tasa de interés anual entre la frecuencia de conversión.

(Tasa de interés anual / Frecuencia de conversión)

Monto compuesto con períodos de conversión fraccionarios

Esta se da cuando el plazo de las operaciones financieras no es múltiplo de la conversión, de manera que no es un número entero, sino un número fraccionario, es decir cuando el tiempo de pago no coincide con el periodo de capitalización.

Regla práctica, comercial o lineal

Consiste en calcular el monto que se acumula durante los periodos de capitalización completos, utilizando la fórmula del interés compuesto, para luego sumarlo con los intereses acumulados durante el periodo incompleto, pero considerando interés simple

Es decir, en esta regla se calcula el monto compuesto para los periodos enteros de capitalización, y se utiliza el interés simple para las fracciones de periodos.

S= C (1 + i) ⁿ x (1 + i x(a/b))

Regla teórica o exponencial

Para esta regla por su parte el monto compuesto se calcula mediante la aplicación del interés compuesto, tanto en la parte entera como en la parte fraccionaria.

S= C (1+ i) ⁿ → S= C (1 + i) ⁿ x (1+i)^a/b

Valor actual o presente al interés compuesto

Este se calcula cuando se conoce el monto que debe pagar o se desea reunir, por lo cual se quiere determinar cual es el capital que es necesario invertir en el tiempo presente a una tasa determinada, esto con el fin de obtener o llegar al monto futuro que se conoce.

Fórmula del Valor Presente

Esta consiste en calcular el valor presente (C o P), que equivale en el presente a una cantidad futura (S o F), ubicada en n periodos adelante (en el futuro), considerando una tasa de interés compuesta (i).

Por lo que en el caso de la formula del valor presente al interés compuesto, se puede determinar utilizando las siguientes fórmulas:

C= S/(1+i)ⁿ o su equivalente C= S (1+i)^-n

Valor presente para periodos de conversión fraccionarios

Cuando el tiempo es una parte fraccionaria del período de conversión el valor presente puede ser encontrado en forma similar al caso de interés compuesto, mediante la regla teórica y la regla práctica.

Regla teórica o exponencial

Consiste en determinar la fracción del período y luego se procede a incluirla en el cálculo.

C= S (1+ i) ^-n → C= S (1 + i) ^-n x (1+i)^-a/b

Regla comercial o práctica

Se calcula el interés compuesto para la parte del plazo y se aplica el interés simple para la parte fraccionaria.

C= S (1+i)^-n x (1+i)

Aproximación de la tasa de interés

Para obtener la aproximación de la tasa de interés es necesario tener los datos del valor futuro, el valor presente, el plazo que corresponde de la obligación financiera y la frecuencia de conversión.

Fórmula de aproximación de la tasa de interés

Por lo cual a continuación se muestra la formula para determinar la tasa de interés compuesto, así que con esta fórmula se determina tasa de interés por periodo de conversión.

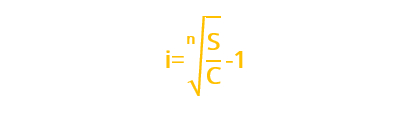
Tasa de interés nominal

Se le conoce también como la tasa contractual, se da cuando el interés es convertible mas de una vez en el año, y se representa con la letra “j”.

Esta se capitaliza varias veces en un año.

Fórmula de tasa de interés nominal

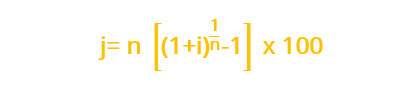
Tasa de interés efectiva

Por su parte a esta tasa también se le llama como rendimiento anual efectivo, esta es la que es ganada en un año, representada con la “i”.

Se define como la tasa interés anual capitalizable una vez al año, es la tasa de rendimiento que se obtiene al cabo de un año debido a la capitalización de los intereses.

Fórmula de tasa de interés efectiva

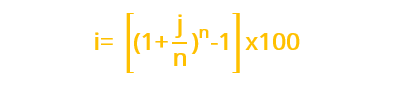
Ejercicios de Interés Compuesto con su respectiva solución

• Una compañía invierte la suma de $34 000 en un fondo de inversión con una tasa de interés del 8,49% convertible trimestralmente durante seis años y medio. Por lo cual se quiere conocer ¿Cuál es el monto compuesto al cumplirse la fecha de vencimiento? Además, ¿Cuánto corresponde a intereses?

• Suponer que se quiere tener al cabo de tres años $12 500, ¿Cuánto dinero debe invertir en un fondo de inversión con una tasa del 9,35% convertible mensualmente?

• Calcular la aproximación de la tasa de interés anual convertible cuatrimestralmente, del monto de $18 000 cuando pase a ser $21 000 en 7 años.

• Hallar la tasa efectiva de interés i equivalente a la tasa nominal de 7% convertible trimestralmente.

• Hallar la tasa nominal j convertible cuatrimestralmente equivalente a una tasa efectiva de 8%.

• Determinar el valor futuro de $4 600, el cual se recibirá dentro de 7 años y 4 meses, con una tasa del interés del 16% convertible semestralmente (Averiguar regla teórica y práctica).

• Hallar el valor presente de $8 700 pagaderos en 6 años y 10 meses suponiendo un rendimiento de 6%, convertible trimestralmente (Averiguar regla teórica y práctica).

Síguenos en nuestras redes sociales estamos como @TodoGerencia en los siguientes enlaces: Instagram, Facebook, Pinterest, Telegram & Twitter.

Documentos de consulta

Ayres, F. (1991). Matemáticas Financieras (Primera ed.). Naucalpan de Juárez, México: McGraw-Hill Interaméricana.

Díaz Mata, A., & Aguilera Gómez, V. (2013). Matemáticas financieras (Quinta ed.). México D.F., México: McGRAW-HILL.

Meza Orozco, J. (2011). Matemáticas Financieras aplicadas (Cuarta ed.). Bogotá, Colombia: Ecoe Ediciones.

Portus Govinden, L. (1997). Matemáticas Financieras (Cuarta ed.). Bogotá, Colombia: McGRAW-HILL INTERAMERICANA.

Vidaurri Aguirre, H. (2017). Matemáticas Financieras (Sexta ed.). México D.F., México: Cengage Leaning.

Villalobos, J. (2007). Matemáticas financieras (Tercera ed.). México D.F., México: Pearson Educación.