Tabla de Amortización: Conceptos, Ejercicios Resueltos y Ejemplos en Excel

A través de este artículo se mostrará cómo es una Tabla de Amortización y como elaborarla, además de calcular las cuotas de amortización, las tasas de interés, los saldos insolutos, los plazos y conceptos importantes sobre las amortizaciones.

Este proceso financiero lo vemos muy presente en diferentes actividades humanas, como cuando se realiza un préstamo hipotecario para una casa, compra de un vehículo o cualquier tipo de crédito, por lo que es importante comprender que muchas deudas se liquidan mediante un pago único en la fecha de vencimiento; sin embargo, es común que los créditos como los antes mencionados y otros de cualquier índole se contraten para pagarlos mediante abonos o pagos parciales. En ambos casos se dice que el préstamo se amortiza.

Significado de Amortización

Es así como desde el punto de vista en las finanzas la Amortización significa el proceso financiero de pago mediante el cual se saldará gradualmente una deuda, esto por medio de una serie de pagos, o sea pagos periódicos que, generalmente, son iguales y que se realizan también a intervalos iguales de tiempo.

Entonces de esta forma comprendemos que la Amortización significa que se paga una deuda y sus intereses mediante ya sea un pago único o mediante una sucesión de pagos parciales que, por lo general, son periódicos, los cuales pueden ser iguales o diferentes en cantidad.

A los pagos parciales también se les llama abonos, cuotas, mensualidades (si los pagos son mensuales), etcétera. La parte del abono, pago parcial o cuota que se destina a reducir la deuda recibe el nombre de Amortización.

En otras palabras, en las amortizaciones de una deuda, cada pago o cuota que se entrega sirve para pagar los intereses y reducir el importe de la deuda.

Por ejemplo, en el caso de los créditos este pago periódico es conocido como abono o cuota del crédito, el cual está compuesto por dos elementos: los intereses del préstamo y la amortización principal.

Abono = Amortización + Intereses generados en el período

El monto que amortiza o disminuye el principal se conoce como amortización.

Aunque esta igualdad de pagos y de periodicidad es lo más común, también se llevan a cabo operaciones con ciertas variantes, por lo que aquí se analizan algunas de estas situaciones.

Principio básico de las amortizaciones

“El interés debe cancelar al final de cada periodo calculado sobre el saldo de los capitales adeudados. En las prácticas comerciales suelen introducirse modificaciones en los sistemas de amortización de pago de intereses vencidos sobre saldos insolutos; estas modificaciones, que en adelante se denominan variantes espúreas (ilegítimas o fraudulentas), tienen el objeto disimulado de obtener intereses a tasas mayores que las pactadas en el documento”

(Portus Govinden, 1997, pág. 292)

Sistemas de amortización

Es importante señalar que, en sistemas o formas para amortizar una deuda, existe una variabilidad según la creatividad de cada persona que se dedica al sistema financiero como por ejemplo al prestar dinero, por lo que trataremos de abarcar aquellos que son más comunes, con sus características, ventajas y desventajas.

Sistema de amortización francés

En la amortización gradual también conocido como método francés, los pagos son iguales y se hacen a intervalos iguales de tiempo, además es la forma de mayor aplicación en el campo financiero.

En este sistema de amortización el saldo insoluto se ve reducido en cada abono, los intereses también se reducen y por lo tanto la amortización se incrementa, siendo entonces mayor que la del pago anterior.

Es importante mencionar según lo anterior que una de las desventajas que presenta este sistema es que los pagos deben ser mayores que los intereses del primer periodo, sino de otra manera no se cancelaria la deuda en su totalidad.

Se define como un sistema por cuotas de valor constante, con intereses sobre saldos, por lo tanto, la amortización gradual, como lo dice su nombre significa que la deuda por pagar se hace de tal manera que la cantidad destinada a reducir el capital aumenta gradualmente, mientras que los abonos o cuotas realizadas son siempre iguales.

Tabla de amortización: Sistema de amortización francés

“En la amortización francés o gradual el abono o cuota constante se calcula despejando A de la fórmula del valor presente de una anualidad, sea vencida o anticipada. Cada abono efectuado se divide en dos partes: en primer lugar, se pagan los intereses que se adeudan al momento en que se efectúa el pago, y el resto se aplica a disminuir el capital de la deuda. Como cada pago reduce el capital, los intereses que se pagan en cada período van disminuyendo; por lo tanto, resulta evidente que la amortización gradual de una deuda se lleva a cabo calculando los intereses sobre el saldo insoluto” (Vidaurri Aguirre, 2017, pág. 363)

• Una persona decide obtener un préstamo por la suma de $32 000 la cual se va a amortizar por un plazo de 18 meses, los cuales serán en pagos iguales. Calcule el abono mensual que debe realizar si la tasa de interés es del 28% capitalizable mensualmente.

Datos:

Crédito= $32 000

Tasa= 28% anual → 2,33% mensual

Plazo= 18 meses

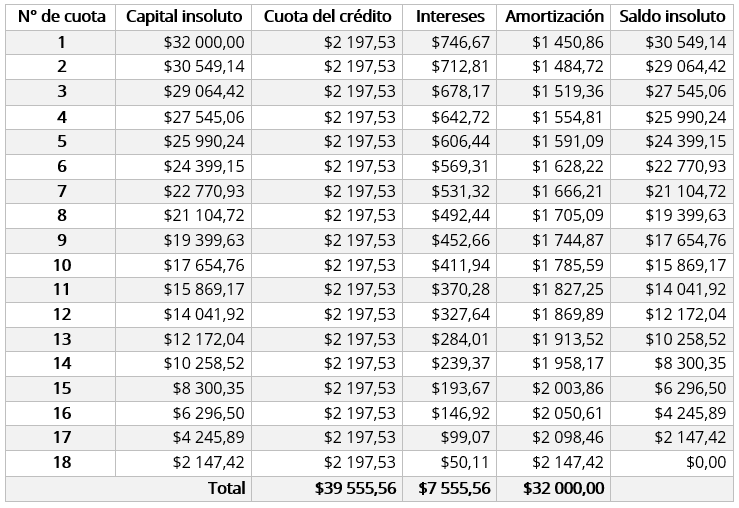
Sistema de amortización alemán

Este método también se le llama amortización constante y se basa en los saldos insolutos o también conocidos como intereses sobre saldo deudor. En este los intereses se cobran sobre el saldo que va quedando después de realizado un abono, por lo cual esto se le conoce como amortización con intereses sobre saldos insolutos.

En el sistema de amortización alemán la porción que se abona al capital, es decir, la amortización, es siempre la misma, o sea se mantiene un valor igual para la amortización en cada periodo, por lo que la cuota de pago periódico es variable decreciente, que quiere decir que cada pago es menor que el anterior, así como los intereses sobre saldos son decrecientes y esto puede ser un atractivo para el deudor. Estos intereses se calculan sobre el saldo insoluto, el cual disminuye con cada amortización

Además, es muy fácil calcular el saldo insoluto en cualquier momento, lo cual, como se dijo antes, se necesita para cancelar o refinanciar el capital que se debe.

Para préstamos a largo plazo, y en particular para préstamos de vivienda, se han creado diversos sistemas de amortización basados en las anualidades variables.

Tabla de de amortización: Sistema de amortización alemán

La amortización para que sea constante precisa de ser calculada dividiendo el capital original entre el número de períodos de pago.

• Se puede comprar un vehículo en 23 mensualidades, el cual tiene un valor de $28 000, más intereses de un 19,5% anual capitalizables mensualmente.

Datos:

Crédito= $28 000

Tasa= 20% anual → 1,63% mensual

Plazo= 23 meses

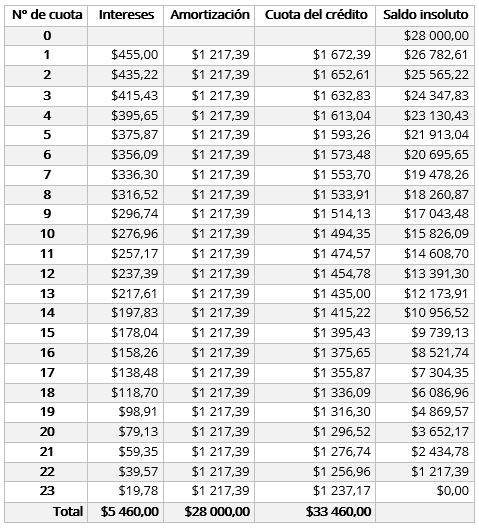
Fondo de amortización

En los fondos de amortización el valor de la deuda se plantea a futuro, por lo que se tienden a realizar depósitos periódicos en alguna inversión, de manera que se acumule la cantidad necesaria para el momento en que es necesario pagar.

“En el método de fondo de amortización para liquidar una deuda, el acreedor recibe el interés pactado en su vencimiento y el valor nominal de la deuda al término del plazo. Con el objeto de poder hacer el último pago, el deudor crea un fondo por separado en el cual hace depósitos periódicos iguales durante el plazo, de tal forma que justamente después del último depósito, el fondo importa el valor de la deuda original. Es de suponerse que el fondo gana intereses, pero no necesariamente a la misma tasa que carga el acreedor “ (Ayres, 1991, pág. 97)

Esto lo vemos reflejado en un caso en el que al deudor le puede resultar difícil o imposible liquidar el dinero con un desembolso único al final, por lo que a través del fondo de amortización tendrá la opción de realizar pagos parciales en una cuenta de este tipo.

Razones por las que se establecen los fondos de amortización

• Para pagar una deuda o préstamo que vence en fecha futura
• Otra es la compra de un equipo nuevo u otro activo que vaya a sustituir al depreciado u obsoleto
• También pagar la educación universitaria de algún miembro de la familia
• Por último la compra de un vehículo

Tabla de amortización: Fondo de amortización

A continuación, a través de un ejercicio veremos reflejado como hacer una tabla de amortización del fondo de amortización.

• La vida útil de un equipo industrial que acaba de ser adquirido por una compañía es de 7 años. A fin de reemplazarlo al final de este tiempo, la empresa establece un fondo de amortización efectuando depósitos anuales vencidos en una cuenta bancaria que paga el 10,5% anual. Si se estima que el equipo industrial costará $1 780 000, calcule el valor del depósito anual.

Datos:

Monto a amortizar= $1 780 000

Tasa= 10,5% anual

Plazo= 7 años

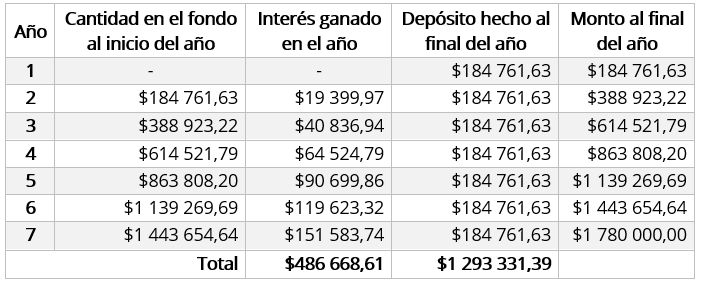
Síguenos en nuestras redes sociales, estamos como @TodoGerencia en los siguientes enlaces: Instagram, Facebook, Pinterest, Telegram & Twitter.

Documentos de consulta:

Ayres, F. (1991). Matemáticas Financieras (Primera ed.). Naucalpan de Juárez, Ciudad de México, México: McGraw-Hill Interaméricana.

Díaz Mata, A., & Aguilera Gómez, V. (2013). Matemáticas financieras (Quinta ed.). México D.F., México: McGRAW-HILL.

Meza Orozco, J. (2011). Matemáticas Financieras aplicadas (Cuarta ed.). Bogotá, Colombia: Ecoe Ediciones.

Portus Govinden, L. (1997). Matemáticas Financieras (Cuarta ed.). Bogotá, Colombia: McGRAW-HILL INTERAMERICANA.

Vidaurri Aguirre, H. (2017). Matemáticas Financieras (Sexta ed.). México D.F., México: Cengage Leaning.

Villalobos, J. (2007). Matemáticas financieras (Tercera ed.). México D.F., México: Pearson Educación.